近年来,理论化学动力学领域的一项核心任务是发展可靠的轨线动力学方法,以在分子模拟中纳入原子核的量子效应。这项研究的重要性源于基于波函数的方法在面对复杂分子时计算量随体系尺寸增大呈指数级增长,导致计算代价难以承受的“维数灾难”。原子核量子效应在许多复杂的化学和生物体系中扮演着至关重要的角色。与此同时,当体系的不同电子态势能面非常接近甚至出现简并时,电子态之间的耦合效应变得不可忽视。这直接导致了玻恩-奥本海默近似的失效,原子核与电子的运动无法完全分离,从而引发不同电子态之间的无辐射跃迁,形成非绝热过程。这类过程广泛存在于光催化反应、光合作用、电子转移、光电转换以及光驱分子马达等领域的重要反应中。通过基于轨线的非绝热动力学模拟,我们有望深入揭示这些过程背后的光化学机理,并为相关应用提供坚实的理论基础。
目前,主流的轨线非绝热动力学方法可分为两大类。第一类基于平均场近似,即轨线在不同电子态加权平均生成的平均场势能面上运动,其理论根源可追溯到量子力学中的Ehrenfest定理。尽管传统的Ehrenfest动力学方法存在相当大的局限性,但基于Meyer和Miller于1979年提出的映射哈密顿量发展起来的一系列平均场方法在凝聚相体系的描述取得了显著成功。由此发展出的平均场方法在各类凝聚态量子开放系统表现出优异的性能。然而,平均场方法在体系离开耦合区域后无法自然恢复玻恩-奥本海默动力学的形式,导致无法描述原子核运动的分支现象,从而限制了其在气相分子非绝热反应过程中的应用。第二类方法是由Tully等人从上世纪70年代起发展的面跳跃动力学。该方法基于单个电子态的玻恩-奥本海默动力学来描述动力学过程,通过耦合区域内轨线在不同电子态间发生的跳跃来描述非绝热效应。虽然面跳跃动力学在离开耦合区域后可以自然地退化成玻恩-奥本海默动力学的形式,对气相体系的模拟相对较佳,但由于原子核在耦合区域不能直接感受到电子自由度的反馈,其对于耦合区域宽广的凝聚相体系的描述往往存在很大缺陷。
近期,伊人直播 刘剑课题组在J. Chem. Theory Comput.上发表综述,系统阐述了一种全新的轨线非绝热动力学方法——非绝热场(nonadiabatic field, NaF)方法的最新进展。与传统方法截然不同,非绝热场中的原子核受力由两部分组成:一是单一电子态势能面提供的绝热力,二是由不同电子态间的非绝热耦合贡献的非绝热力(J. Phys. Chem. Lett. 2024, 15, 644−658;J. Phys. Chem. Lett. 2024, 15, 5452−5466)。在耦合区域内,电子态之间的相干性可以通过非绝热力直接反馈给原子核;而当体系离开耦合区域后,由于非绝热耦合消失,非绝热力不再对原子核的运动有贡献,非绝热场自动退化为玻恩-奥本海默动力学形式,从而能够准确描述原子核的分支效应。这一特性使非绝热场方法在耦合区域和非耦合区域内均能展现出正确的物理图像。综述不仅回顾了非绝热场方法的早期理论框架,还重点介绍了以下两项重要进展: 1)通过理论分析,推导出非绝热场所采用的能量守恒形式在无穷小时间步长下对应的运动方程。在此方程中,非绝热力被投影至垂直于原子核速度的方向,形成了有效非绝热力。这一运动方程的解析解结合优化的数值积分方案,显著提升了非绝热场的稳定性与计算效率; 2)对于定义在透热表象中的模型体系,将非绝热场的原子核受力重新表达于透热表象下,直接在透热表象下进行演化,进一步提升了模拟效率。
刘剑课题组前期指出,轨线动力学方法的性能取决于三个核心要素:轨线运动方程、初始条件和物理量的计算形式。位置-动量相空间表示是量子力学的一种严格诠释形式,也是经典力学的一类基本理论,可以作为天然的桥梁来发展量子力学的轨线动力学方法。刘剑课题组基于离散量子态空间的封闭性提出了关于位置-动量相空间映射哈密顿量的统一理论框架(J. Chem. Phys. 2016, 145, 204105; J. Chem. Phys. 2017, 146, 024110),并随后建立了离散量子态自由度的约束位置-动量相空间理论和针对非绝热体系的广义位置-动量相空间理论(J. Chem. Phys. 2019, 151, 024105; J. Phys. Chem. Lett. 2021, 12, 2496−2501; J. Phys. Chem. A 2021, 125, 6845−6863; Acc. Chem. Res. 2021, 54, 4215−4228; Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1619)。在非绝热场方法中,后两个要素由广义位置-动量相空间表示决定。其中,原子核自由度以传统的Wigner相空间描述,电子自由度则通过约束位置-动量相空间刻画。当电子自由度的映射核和逆映射核对任意酉变换均具有协变性,该方法称为协变-协变非绝热场方法(NaF-cc)。刘剑课题组进一步将Cotton和Miller发展的三角窗函数在约束位置-动量相空间表示下重新诠释和进一步发展,严格证明了其对孤立二态量子系统的准确性(Chin. J. Chem. Phys. 2024, 37, 230−254),并与NaF结合提出了NaF-TW方法,彻底解决了布居数正定性问题(J. Phys. Chem. Lett. 2024, 15, 5452−5466)。近期,刘剑课题组进一步采用微分流形理论重新表述了约束位置-动量相空间表示理论(arXiv: 2503.16062),指出其流形结构与复Stiefel流形对应,并在此基础上发展了多种描述电子自由度的位置-动量相空间形式。在该文中,刘剑课题组将这些新的相空间表示与NaF方法结合,发展出多种新型NaF方法,包括基于丘形窗函数的NaF(NaF-HW)和基于非协变逆映射核的NaF(NaF-cx)。这些NaF方法在多个典型模型体系中进行测试,并与严格的量子动力学结果及三种代表性的面跳跃动力学方法进行了比较。
对于气相体系的测试,图1-3展示了描述吡嗪和胸腺嘧啶分子锥形交叉的线性振动耦合模型和两态的非谐光解离模型的模拟结果。图1显示,各类NaF方法与面跳跃动力学对吡嗪模型的电子态布居数和原子核的动力学均能给出合理的描述。然而,图2中胸腺嘧啶分子模型的布居数动力学中,面跳跃动力学方法未能精确描述布居数转移行为,而各种NaF方法表现远为出色。对于两态光解离模型(图3),NaF方法的预测与严格数值结果几乎一致,而面跳跃动力学方法则存在定量描述上的明显误差或者定性错误的非物理震荡现象。这些结果表明,NaF方法可以胜任气相分子体系的非绝热动力学模拟,对电子和原子核的动力学描述都表现出卓越的稳健性。
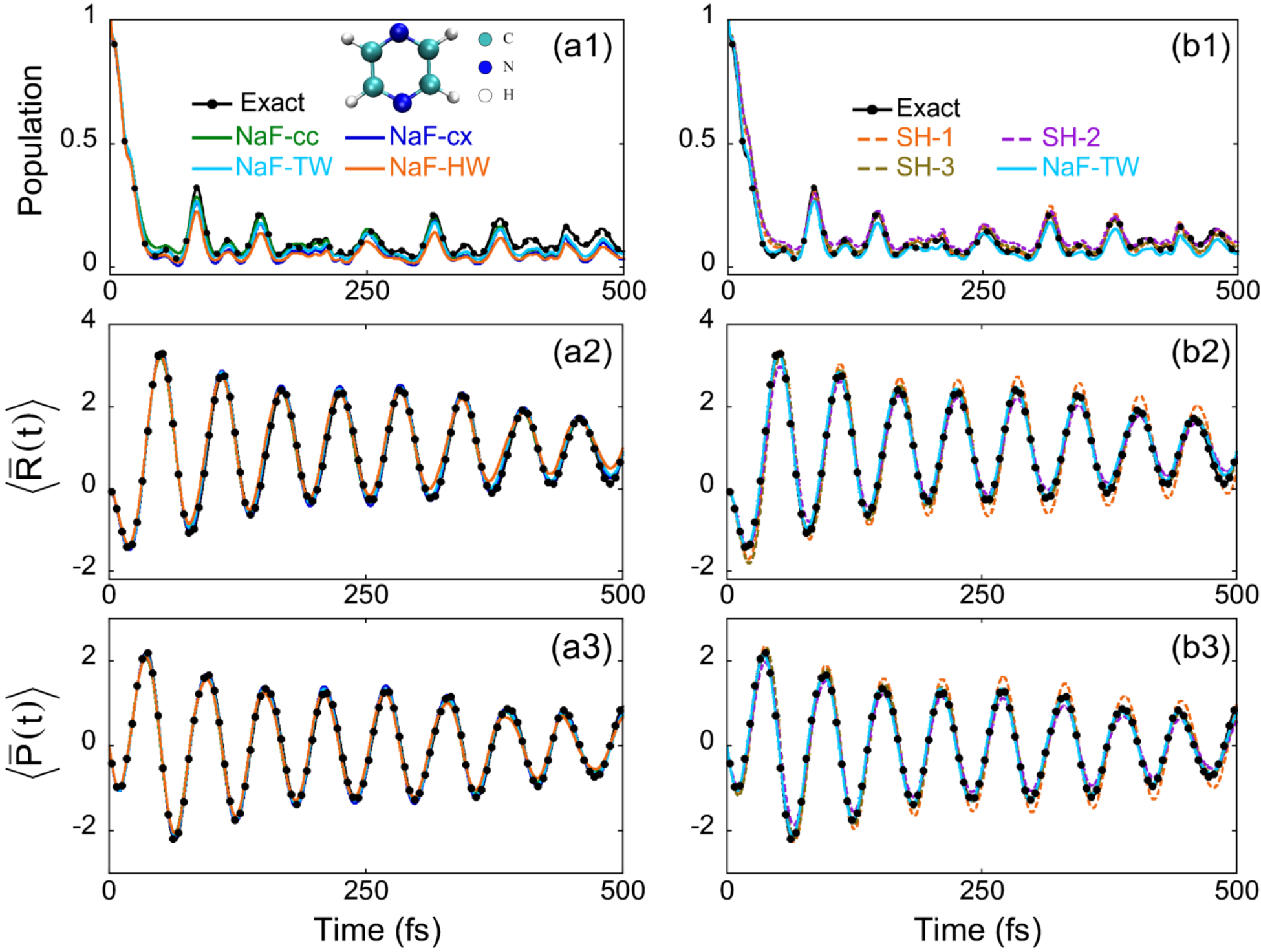
图1. 吡嗪的两态24模式线性振动耦合模型的动力学结果。从上至下三行分别是第二个电子态的布居数、原子核的位置平均值和动量平均值随时间变化的结果。图(a1)-(a3)中,绿色、蓝色、青色和橙色实线分别代表NaF-cc, NaF-cx, NaF-TW和NaF-HW的结果。图(b1)-(b3)中,橙色虚线、紫色虚线、棕色虚线和青色实线分别代表SH-1,SH-2,SH-3和NaF-TW的结果。各自图中的黑色圆点+实线代表数值严格的MCTDH的结果。
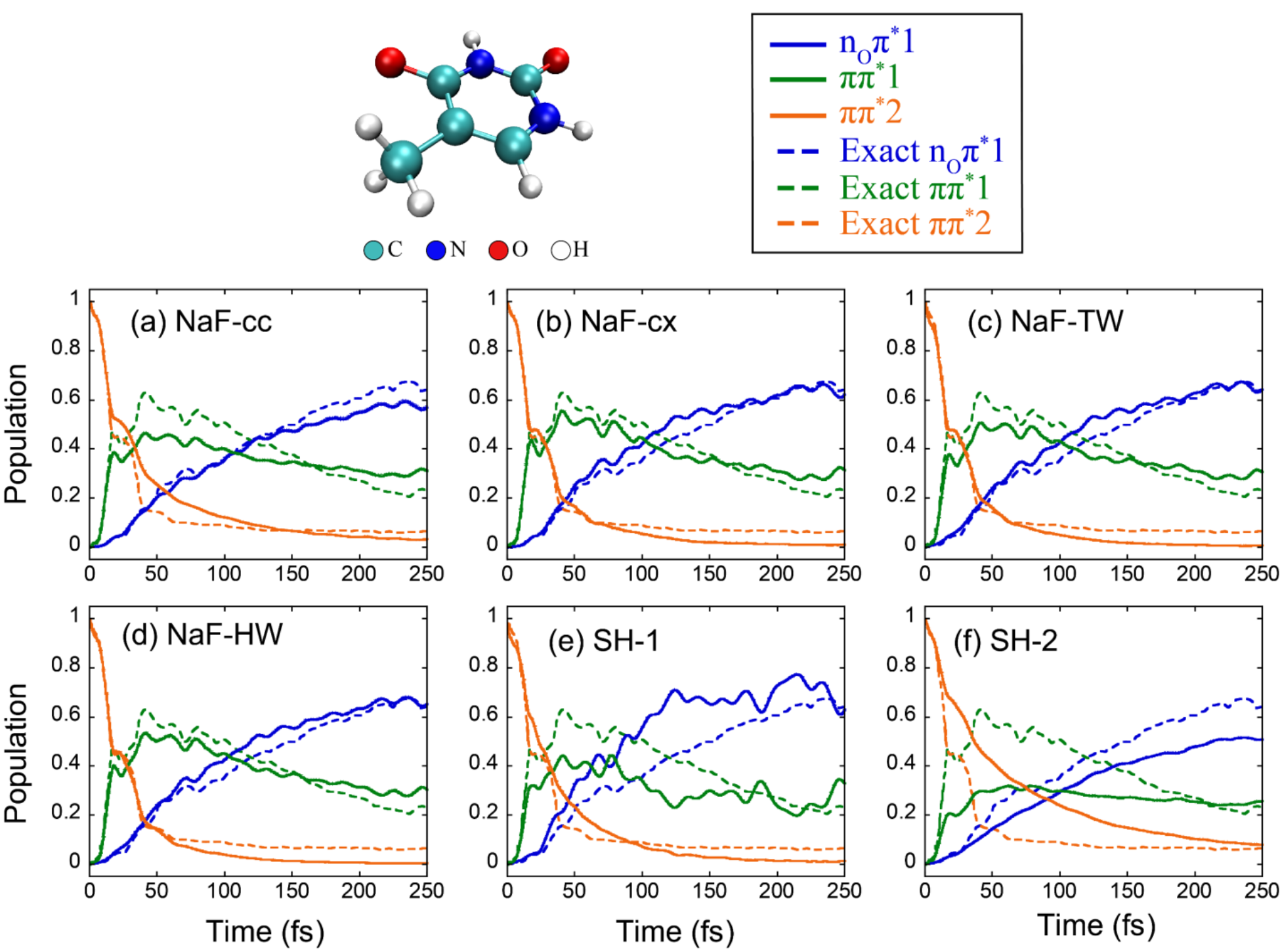
图2. 胸腺嘧啶的线性振动耦合模型的布居数动力学结果。实线和虚线分别代表轨线方法和数值严格的ML-MCTDH的结果,其中蓝色、绿色和橙色分别表示三个不同的电子态。 (a): NaF-cc; (b): NaF-cx; (c): NaF-TW; (d): NaF-HW; (e): SH-1; (f): SH-2。由于SH-3只能用于两态体系,因此无法给出此七态体系的模拟结果。
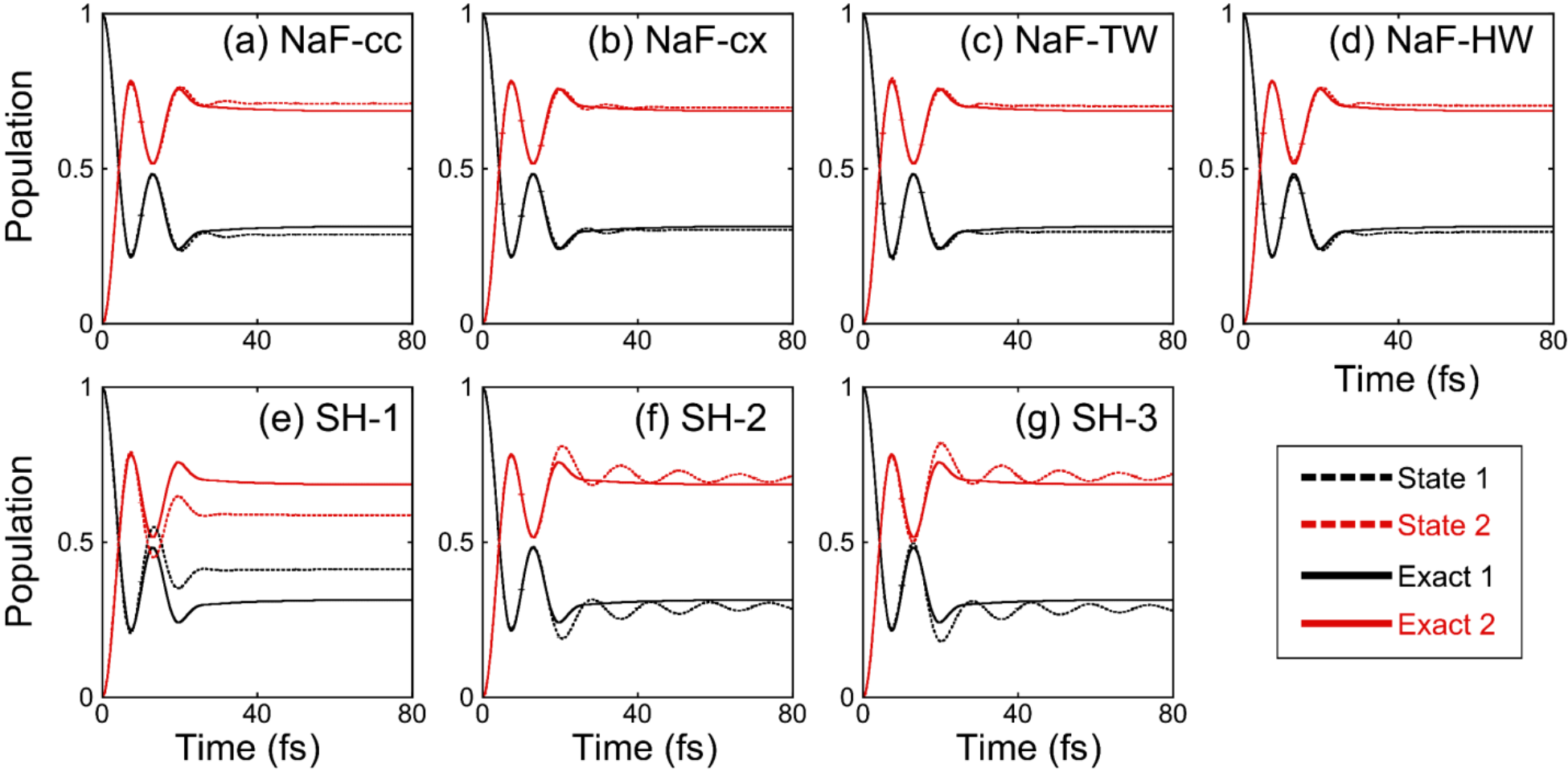
图3. 两态非谐光解离模型的布居数动力学结果。虚线和实线分别代表轨线方法和数值严格的ML-MCTDH的结果,其中黑色和红色分别表示第一个和第二个电子态。 (a): NaF-cc; (b): NaF-cx; (c): NaF-TW; (d): NaF-HW; (e): SH-1; (f): SH-2; (g): SH-3。
对于非绝热耦合区域更为宽广的凝聚相体系,图4为77 K下用于描述光合作用位点蛋白复合物的FMO模型的布居数动力学。以数值严格的含时密度矩阵重正化群(TD-DMRG)方法的精确结果作为参考,NaF方法不仅能够给出合理的短时布居数的转移行为,对长时布居数的平衡状态的描述也表现出令人满意的性能。图5进一步表明,在原子核量子效应更为显著的零温条件下,NaF方法依然与TD-DMRG结果高度一致。相比之下,面跳跃动力学方法表现出显著的定性偏差。此外,图6展示了两态腔中原子模型的布居数动力学。不同的面跳跃动力学方法在描述短时的自发辐射行为以及长时的重吸收/重发射现象时出现与严格数值结果的明显偏差。而多种NaF方法始终能够与严格数值结果保持自洽一致。这些现象说明相比于面跳跃动力学,包含了非绝热力以及结合了量子相空间表示的NaF对耦合区域宽广的凝聚态体系的描述更有显著优势。
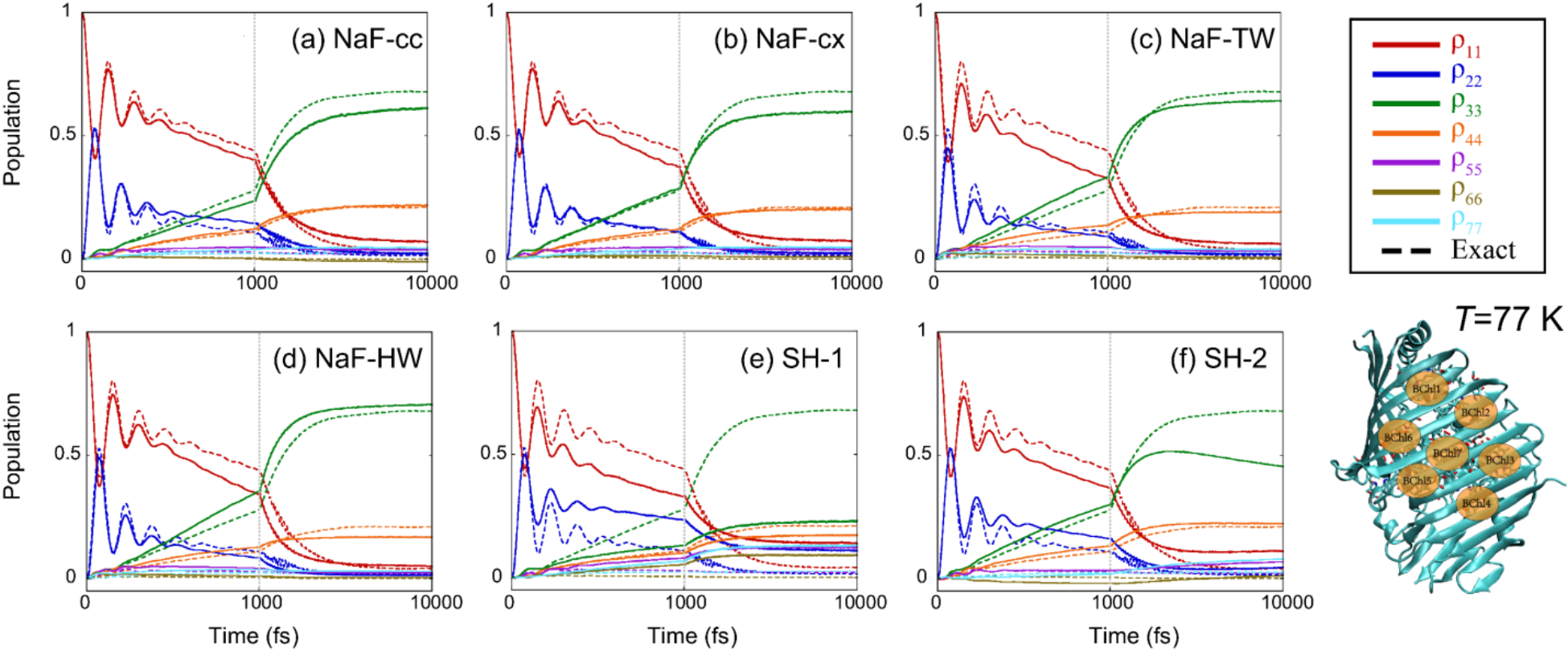
图4. FMO模型在77 K下的布居数动力学结果。红色、蓝色、绿色、橙色、紫色、棕色和青色实线分别表示轨线给出的七个电子态的布居数结果。 (a): NaF-cc; (b): NaF-cx; (c): NaF-TW; (d): NaF-HW; (e): SH-1; (f): SH-2。由于SH-3只能用于两态体系,因此无法给出此七态体系的模拟结果。数值严格结果由TD-DMRG模拟得到,以相应颜色的虚线绘制在各子图中。

图5. FMO模型在零温下的布居数动力学结果。红色、蓝色、绿色、橙色、紫色、棕色和青色实线分别表示轨线给出的七个电子态的布居数结果。 (a): NaF-cc; (b): NaF-cx; (c): NaF-TW; (d): NaF-HW; (e): SH-1; (f): SH-2。由于SH-3只能用于两态体系,因此无法给出此七态体系的模拟结果。数值严格结果由TD-DMRG模拟得到,以相应颜色的虚线绘制在各子图中。
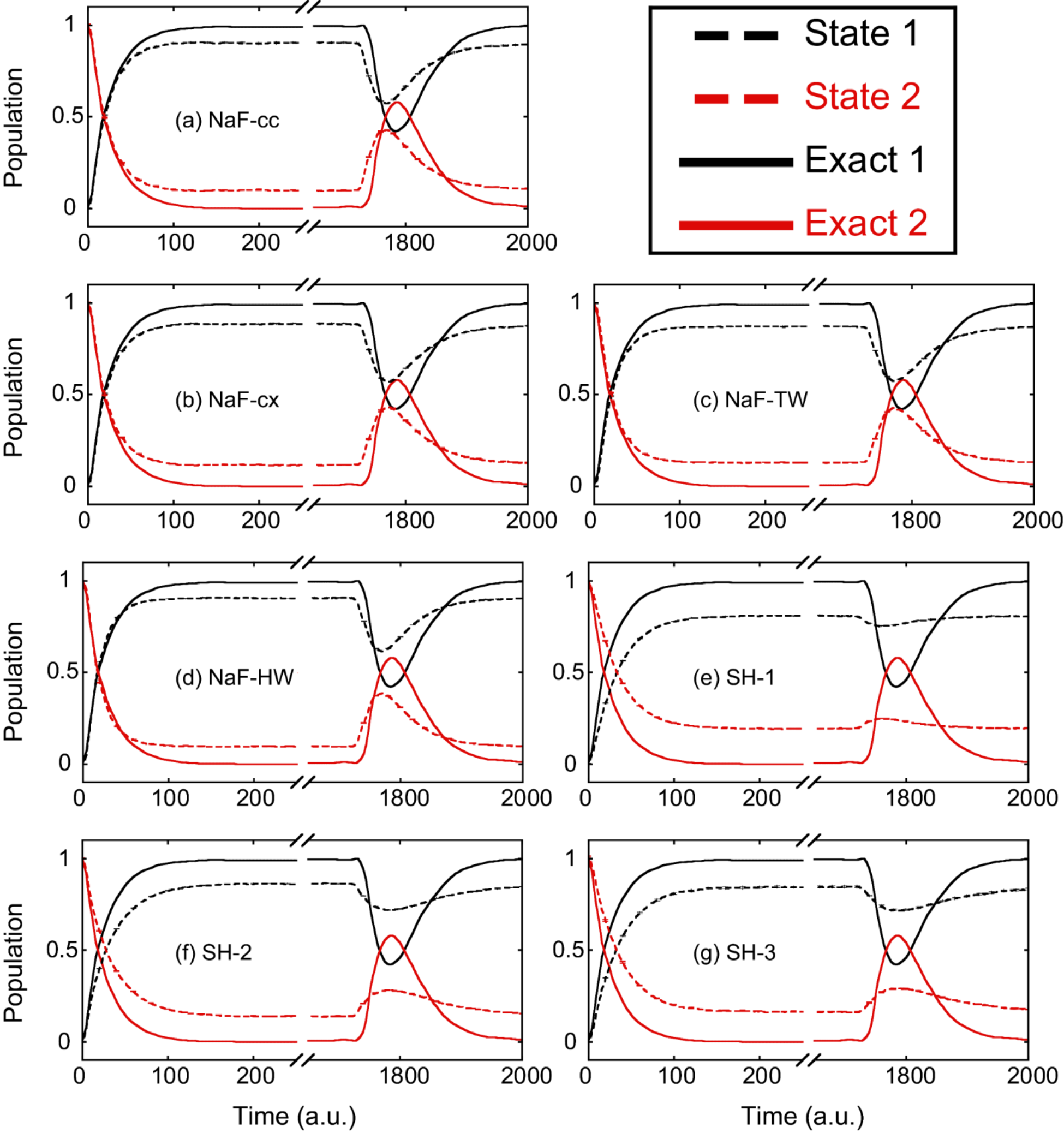
图6. 腔中原子模型的布居数动力学结果。虚线和实线分别代表轨线方法和数值严格方法给出的结果,其中黑色和红色分别表示原子的基态和激发态。 (a): NaF-cc; (b): NaF-cx; (c): NaF-TW; (d): NaF-HW; (e): SH-1; (f): SH-2; (g): SH-3。
此外,NaF方法在电子相干动力学、单线态裂分、有机半导体Holstein模型等复杂体系中也表现出色,展现了其应用于各类复杂非绝热过程的巨大潜力。
综上所述,非绝热场(NaF)作为一种概念全新的轨线非绝热动力学方法,为非绝热体系的模拟提供了新思路。借助广义位置-动量相空间表示的量子理论,非绝热场不仅能够胜任气相分子体系的非绝热动力学模拟,还在耦合区域宽广的凝聚相体系数值模拟中展现出显著优势。通过结合ab initio计算或机器学习技术,非绝热场有望成为真实复杂体系非绝热过程模拟的强大工具,为光化学过程的深入理解和实际应用奠定了坚实的理论基础。此外,文中展示的多种模型体系测试实例涵盖了非绝热过程的不同情形,这些结果为非绝热动力学近似方法的开发提供了重要参考。
伊人直播-伊人直播ios 刘剑教授为通讯作者,伊人直播-伊人直播ios 博雅博士后吴柏华,三年级研究生李炳其,已毕业博士生贺鑫,四年级研究生程祥松和北京师范大学伊人直播 任佳骏副教授为文章合作作者。 该工作得到了国家杰出青年科学基金项目(项目号: 22225304)的资助。计算资源由北京并行科技、广州超级计算中心、伊人直播 高性能计算平台以及崂山实验室(LSKJ202300305)提供。
论文信息:
“Nonadiabatic Field: A Conceptually Novel Approach for Nonadiabatic Quantum Molecular Dynamics”
Baihua Wu†, Bingqi Li†, Xin He†, Xiangsong Cheng, Jiajun Ren, Jian Liu*. Journal of Chemical Theory and Computation,2025,21, 8, 3775–3813.//doi.org/10.1021/acs.jctc.5c00181
Related nonadiabatic field software for heterogeneous hardware: